Continuous time Markov Chains Cellular Network Design Solution
Introduction
The COVID-19 pandemic has forced governments, municipalities, and other institutions worldwide to implement strict countermeasures against the transmission of the disease. In addition to hygiene countermeasures, such as mouth rinsing and hand washing, it is important to stop crowd gatherings [1]. The increased use of online platforms has helped alleviate this issue but has resulted in changes to the existing physical environments, thus facilitating the requirement for objective indicators to determine the crowdedness of a given facility.
Measuring crowdedness is important for developing COVID-19 countermeasures and optimizing crowdedness to help overcome imbalances in the number of customers congregating in a certain area of interest. In the transportation field, the effects of crowdedness have been documented from the perspectives of accessibility and mobility [2]. Cameras have been increasingly used to analyze the movements of people in buses and other similar settings in recent years [3, 4]. However, it is difficult to analyze simultaneous events at multiple points since cameras capture only a specific point in space.
Global internet usage reached approximately 63% in 2021, making it an indispensable part of our daily lives [5]. The increasing usage of smartphones worldwide is primarily attributed to the increased internet connectivity over both mobile networks and Wi-Fi. The Wi-Fi environment presents various applications and is used in education, tourism, and disaster management and prevention, leading to the establishment of national Wi-Fi policies in several countries across the world. The Wi-Fi environment is the most preferred network environment owing to the advent of 5G and other technologies and is expected to be used widely in virtual reality, remote offices, online classes, and various other fields, such as smart homes, support for the elderly, and nursing care [6,7,8,9].
In this study, we propose an optimization method to avoid crowding in facilities, thereby limiting the transmission of COVID-19. We analyze Wi-Fi logs created regularly across different Wi-Fi environments to determine the behavior of the users. In the proposed method, the constraints set ensure that users and facility managers can take realistic steps against crowdedness without drastically changing the status quo. Firstly, we used Wi-Fi log statistics to perform a basic analysis of Wi-Fi users. We then classified users based on factors, such as frequency of use, location, and stay time, and identified the user groups present in the facility. Subsequently, we obtained information on the transition probabilities between nodes and the stay time at each node for each user group, which were modeled as a continuous-time Markov chain. If a stationary distribution was obtained, the variance of the stationary distribution was used as a metric to assess the intra-facility crowdedness. We then performed optimization under certain constraints, considering the stay time parameter of each node as the explanatory variable and the variance of the stationary distribution as the objective function. This approach can help in alleviating crowdedness in practical conditions. The proposed optimization method effectively utilizes Wi-Fi environment logs to help facility operators limit the transmission of COVID-19.
Related work
Extensive research has been conducted on determining user behavior using Wi-Fi logs in various fields [10,11,12,13,14,15,16,17,18,19,20,21]. In particular, studies have been conducted on tourism behavior analysis using Wi-Fi logs to better understand the state of tourism behavior based on facility and visitor stay times and OD (Origin–Destination) Tables [22, 23]. For example, Internet-of-Things (IoT) data transmitted through Bluetooth and Wi-Fi have been used to monitor and estimate the number of passengers and the waiting time for buses and subway trains [24, 25]. Wi-Fi data have also been used to track tourists and determine the appeal of tourist attractions [26]. This Wi-Fi data tracking enables a strategic implementation of services, including estimating factors affecting tourism and presenting recommendations to tourists [27, 28]. However, these applications have not accelerated the use of Wi-Fi data for strategic planning thus far.
In previous studies, Markov chains were used to understand tourism behavior [29, 30]. These studies did not consider properties such as reachability or stationary distribution as they were based on the concept of absorbing Markov chains, wherein the user arrives from outside. Additionally, data-cleaning methods have been examined owing to the large volume of Wi-Fi log data [31]. However, the research conducted on the computing environment and the methods used to analyze large quantities of log data has been limited. The computing environment which handles the ever-increasing log data is significant for achieving real-time results. The Wi-Fi logs provided by vendor tools typically include basic information, such as the number of user connections, connecting devices, authentication status, and usage status. The arrival rate per unit time and the stay time of each user can be obtained. However, the vendor-supplied tools do not track user transitions through access points, which limits their ability to present a detailed overview of user trends.
Several efforts have been made to mitigate the impact of the COVID-19 pandemic, including investigating and predicting infection and movement of people [32, 33]. Ainslie et al. [34, 35] observed a strong correlation between intra-urban migration and the infection rate based on the intra-city movement data obtained during the early stages of the pandemic. In addition, susceptible, infected, and recovered (SIR) models have been used to investigate and predict the infections [9, 36,37,38].
IoT devices have also been used to monitor and intervene in public health in densely populated areas. A recent study incorporated machine learning approaches to maximize the testing resources to track people that have come into contact with an infected person [39,40,41]. Wang et al. [42] observed that interventions focusing on highly-mobile individuals and popular locations rather than the movements of actual people captured by Wi-Fi and GPS could reduce both peak infection rates and the total number of infected people while maintaining high social activity levels. However, none of these studies have attempted the optimization of crowdedness.
In this study, we have developed an environment wherein Wi-Fi logs can be analyzed realistically, and we propose a method to define and optimize intra-facility crowdedness. This approach enables the implementation of realistic anti-crowding measures and addresses the issues surrounding the global COVID-19 pandemic.
Features of this study
This study focuses on the environment along with analyzing large amounts of Wi-Fi logs and calculating their statistics. Table 1 presents a comparison of the findings of this study with that of a previous study. The left side of the table presents items related to the scale of the Wi-Fi logs, while the right side presents items related to the analysis. In addition to basic statistical methods, clustering of users is also important to analyze the logs, which present a better understanding of the trend of Wi-Fi users. Further optimization can help in the development of an improved environment. This study utilizes a sufficient amount of Wi-Fi logs for analysis, along with a log calculation flow and large-scale computing environment. The proposed analysis method presents considerable academic and practical significance as it enables system optimization through statistical analysis and user classification.
Materials and methods
In this study, we used Wi-Fi logs to optimize the intra-facility crowdedness. This section details the proposed approach for processing large quantities of Wi-Fi logs and the computing environment needed. We calculated the characteristics of different users and organized them into groups using the characteristic quantities obtained from the processed Wi-Fi logs. We then used these user groups to assess intra-facility crowdedness based on a continuous-time-type Markov chain. Lastly, we developed an optimization model which minimizes the intra-facility crowdedness. The optimization model imposes a fixed limit on the variability of the stay time by using the stay time of the user as a parameter, making it a realistic solution. Congestion in a facility can be avoided using two methods: (1) changing the flow lines within the facility, and (2) changing the time spent within the facility. However, method (1) requires major changes to both the customers and the facility. However, method (2) requires changes only to the length of stay, and the facility remains largely unaffected. Furthermore, in the absence of a constraint to reduce congestion, the facility would simply reduce it, thereby reducing the value of the facility. Thus, we could match the actual conditions at the facility by using method (2) and setting additional constraints.
Process from Wi-Fi log to transition probability matrix calculation
Items used in the Wi-Fi logs
The WPA2-Enterprise with 802.1X authentication and WPA2-PSK (shared network key) were used as the main security nodes for a basic authentication at a Wi-Fi access point. These authentication methods require the following log items collected by most logging programs and used in this analysis, i.e., connection time, destination access point, and unique user identifier.
Overview of the Wi-Fi log data used
We used the Crawdad.org dataset for our Wi-Fi log data, which is a dataset of association records for the Eduroam network at the KTH campuses, collected during 2014–2015 [43]. Table 2 lists access point (AP) information for this dataset, including AP name and location information. A total of 1,123 APs were listed in the database.
Table 3 lists the content of the file containing user connection information, which includes a unique user identifier, the AP to which the user is connected, and the connection time. Table 4 lists the files in the dataset organized on a monthly basis. The data containing N/A and users with only one connection were excluded. We targeted users who had connected more than once and had transitions between APs.
Calculation of transition probabilities and stay times
The process for calculating the transition probabilities and stay times from the Wi-Fi logs is presented below. This process is a general-purpose workflow for WiFi logs.
- A.
Preprocessing for Wi-Fi log analysis:
- (1)
Delete records containing "N/A" from the original file.
- (2)
Delete users who appear only once in the original file.
- (3)
Output the files processed in (1) and (2).
- (1)
- B.
Main processing for Wi-Fi log analysis:
- (1)
Calculate the transition probabilities through parallel computation by using the Message Passing Interface (MPI), based on the file created in A (preprocessing).
- (2)
Each MPI process calculates the number of transitions and stay times of the specified user and outputs the results to a file with the aggregated information of all the users.
- (1)
- C.
Post-processing for Wi-Fi log analysis:
- (1)
Delete APs with no transitions and calculate the transition probability matrix from the file obtained in B (main processing).
- (2)
Calculate the transition probability matrix and mean stay time for each classroom, floor, and building with the APs aggregated and output the results to a file.
- (1)
Figure 1 illustrates the state transition obtained in Section B. (Main process for calculating transition probabilities).
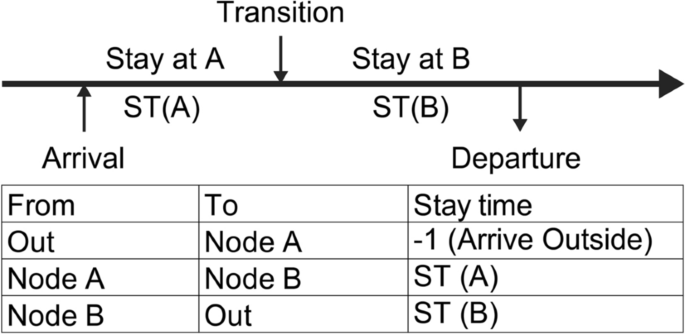
State transition in Wi-Fi logs
Process for calculating user groups
We performed clustering using the k-means method to analyze the characteristics of Wi-Fi users. We created a dataset for each user based on calculation results of transition probabilities and stay times in the format presented below. Here, the node number indicates the number assigned when the AP aggregation is performed. Table 5 presents the information on the environment in which clustering was computed.
User i = {node 1: number of connections …, node N: number of connections, node 1: stay time …, node N: stay time}.
Computing environment for Wi-Fi log analysis
The Wi-Fi logs are enormous, and because the number of access points and users increases, the computation time increases. Therefore, a simple computing environment cannot adequately handle the seamless operation of businesses. Consequently, we used a parallel computing environment to improve the efficiency of the Wi-Fi log computations. Table 6 lists the information on the programming environment used in this study. Additionally, we used the SQUID computing environment [44] at the Cybermedia Center of Osaka University. The file for 2014/09, which possessed the largest number of records, required a computation time of 8836.68 s. The computation time can be further reduced by increasing the amount of parallelism based on the availability of computing resources.
Measuring intra-facility crowdedness from Wi-Fi logs using continuous-time Markov chains
In this section, we first define the facility crowdedness using a continuous-time Markov chain [45]. We assume a finite state space, \(S\), and continuous-time stochastic process, \(\{X\left(t\right);t\ge 0\}\). We define a continuous-time Markov chain with the transition probability, \({\varvec{P}}\left(t\right)= \left({p}_{ij}(t)\right), i,j\in S\) on \(S\). Here, \(X(t)\) is assumed to satisfy the following equation and be synchronous:
$${p}_{ij}(t)= P\left(X\left(s+t\right)=j|X\left(s\right)=i\right), i,j\in S$$
In addition, for each transition probability, \({p}_{ij}(t)\),
$${q}_{i}=\underset{h\downarrow 0}{\mathit{lim}}\frac{1-{p}_{ii}(h)}{h}\in \left[0, \infty \right], i\in S,$$
$${q}_{ij}=\underset{h\downarrow 0}{\mathrm{lim}}\frac{{p}_{ij}\left(h\right)}{h}\in \left[0,\infty \right], i\in S, i\ne j.$$
We define the transition rate matrix assuming \({q}_{ii}=-{q}_{i}, i\in S\), as follows:
$${\varvec{Q}}={(q}_{ij})=\underset{h\downarrow 0}{\mathrm{lim}}\frac{\left\{{\varvec{P}}\left(h\right)-{\varvec{I}}\right\}}{h},$$
where \({\varvec{P}}\left(0\right)={\varvec{I}}\).
At time, \(t\), when \(X(t) = i\) and \(i\in S\), the probability that the remaining stay time, \({\tau }_{i}(t)\), is greater than \(u\) is given by:
$$P\left({\tau }_{i}\left(t\right)>u|X\left(t-\right)\ne i,X\left(t\right)=i\right)={e}^{-{a}_{i}u},$$
where \(\frac{1}{{a}_{i}}\) represents the mean stay time for \(i\in S\). Therefore, the transition rate, \({q}_{ij}\), can be expressed as:
$$\begin{array}{c}{{q}}_{{i}{j}}=\left\{\begin{array}{c}-{{a}}_{{i}} \left({i}={j}\right)\\ {{a}}_{{i}}{{p}}_{{i}{j}} \left({i}\ne {j}\right)\end{array}\right.\end{array}$$
(1)
When \(X(t)\) is irreducible and ergodic, there is a limit distribution for \(j\in S\)
$${\pi }_{j}=\underset{t\to \infty }{\mathrm{lim}}{p}_{ij}\left(t\right)\ge 0, {\sum }_{j\in S}{\pi }_{j}=1,$$
where \({\pi }_{j}\) satisfies:
$$\begin{array}{c}{\sum }_{{i}\in {S}}{{\pi}}_{{i}}{{q}}_{{i}{j}}=0,\boldsymbol{ }\left({j}\in {S}\right)\end{array}$$
(2)
and \({\pi }_{i} (i\in S)\) denotes the stationary distribution.
To define intra-facility crowdedness, we consider \(\sigma\) as the variance of the stationary distribution of each state. Therefore,
$$\sigma \left({\varvec{a}}\right)=\frac{1}{\left|S\right|}{\sum }_{i\in S}{{(\pi }_{i}-\overline{\pi })}^{2},$$
where\(\overline{\pi }=\frac{1}{|s|}{\sum }_{i\in S}{\pi }_{i}\).
Method for optimizing intra-facility crowdedness
Subsequently, we propose a method to optimize the crowdedness of the facilities [46]. In this section, we classify the users based on their usage and introduce a set, \(C\), of the user classes. Intra-facility crowdedness is defined as the variance of the stationary distribution of each state. Therefore, we can reduce the intra-facility crowdedness by minimizing this variance, as shown in Eq. (3). Here, the sum of the mean stay times in the facility is set as a constant value for each user class to avoid any hindrances in the usage of the facility, as shown in Eq. (4). Here, \({{\varvec{a}}}^{\boldsymbol{^{\prime}}({c})}\) denotes the initial value of \({{\varvec{a}}}^{({c})}\), \({\pi }_{i}^{\left(c\right)}\left({a}_{i}^{\left(c\right)}\right)\) denotes the stationary distribution, given the stay rate, \({a}_{i}^{(c)}\), node, \(i\), and user class, \(c\), and \(\overline{\pi }\left({a}_{i}^{\left(c\right)}\right)\) denotes the mean value of the stationary distribution. A drastic change in the stay rate of users may cause confusion; therefore, we limit the change to a certain range for each user class, as shown in Eq. (5).
$$\begin{array}{c}Minimize \quad \sigma \left({{\varvec{a}}}^{\left(1\right)},\dots ,\boldsymbol{ }{{\varvec{a}}}^{\left({c}\right)},\dots \right)=\frac{1}{\left|{S}\right|}\sum_{{c}\in {C}}\sum_{{i}\in {S}}{\left({{\pi}}_{{i}}^{\left({c}\right)}\left({{a}}_{{i}}^{\left({c}\right)}\right)-\boldsymbol{ }\overline{{\pi} }\left({{a}}_{{i}}^{\left({c}\right)}\right)\right)}^{2}\end{array}$$
(3)
$$Subject \quad to \quad {a}_{i}^{(c)}\ge 0, i\in S, c\in C$$
$${\sum }_{i\in S}\frac{1}{{a}_{i}^{(c)}}={K}^{(c)}, {K}^{(c)}\in {\mathbb{R}}$$
(4)
$${{\varvec{a}}\boldsymbol{^{\prime}}}^{(c)}\left(1-{\gamma }^{(c)}\right)\le {{\varvec{a}}}^{\left({c}\right)}\le {{\varvec{a}}\boldsymbol{^{\prime}}}^{\left(c\right)}\left(1+{\gamma }^{\left(c\right)}\right), {\gamma }^{\left(c\right)}\in {\mathbb{R}}$$
(5)
Facility crowdedness optimization algorithm
The facility crowdedness optimization algorithm is as follows:
- (1)
Classify users into classes\(,\) \(C,\) based on facility Wi-Fi logs.
- (2)
For each class, \(c\in C\), \(calculate\) the transition probability matrix, \({{\varvec{P}}}^{c}\left(t\right)=\left({p}_{ij}^{c}\left(t\right)\right), i,j\in S, c\in C\), and set the initial value of the stay time parameter, \({a}_{i}^{(c)}\), based on the flow described in 2.1.3.
- (3)
Create the transition rate matrix, \({{\varvec{Q}}}^{(c)}\), based on Equation (\(1\)) and obtain \({\pi }_{i}^{(c)}\) from Equation (\(2\)).
- (4)
Solve the optimization problem (\(3\)) and determine an \({{\varvec{a}}}^{({c})}\) value which satisfies the conditions.
- (5)
Repeat steps (3) and (4) to calculate the optimal \({{\varvec{a}}}^{({c})}\) value.
Table 7 presents the information on our computing environment used for optimizing the intra-facility crowdedness.
Results and discussion
Basic user analysis obtained from Wi-Fi logs
We categorized the users into five classes based on the number of connections, location, and stay time. Table 8 lists the characteristics of each class. Figure 2 depicts the number of users who used Wi-Fi in each building at least once. Most users belonged to Class 0 and had a short mean stay time. These could be outside users or students who do not regularly use the network as the data used in this study were obtained from Eduroam, which is a Wi-Fi roaming service that allows access from outside the university where it is installed.
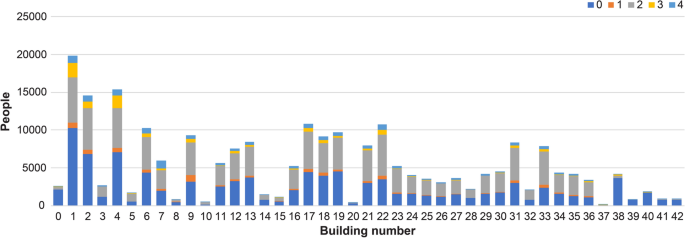
Number of users who used the Wi-Fi in each building node at least once
We clustered the buildings by using the mean stay times of the users in each building (mean stay time for user class 0, mean stay time for user class 1,…, mean stay time for user class 4) to obtain an accurate classification of the characteristics of the user classes. Table 9 presents the results. Except for user class 0, more than 75% of all the user classes were present in building cluster 2 at least once. The table presents the characteristics of each user class, e.g., user class 2 uses building cluster 4, user class 3 uses building cluster 2, and so on.
Evaluation of intra-facility crowdedness by class
We evaluated the intra-facility crowding in each class. Table 10 presents the class-specific values related to intra-facility crowding. The mean stay time (h) was the mean value of stay time in each building for each class. The total mean stay time (h), which is the sum of stay times in each building, is a constraint imposed on the optimization. The intra-facility crowdedness was computed for each class. Class 3 presents the largest mean stay time, the largest sum thereof, and the greatest intra-facility crowdedness.
Figures 3 and 4 depict the stay rate and stationary distribution for each class, respectively.
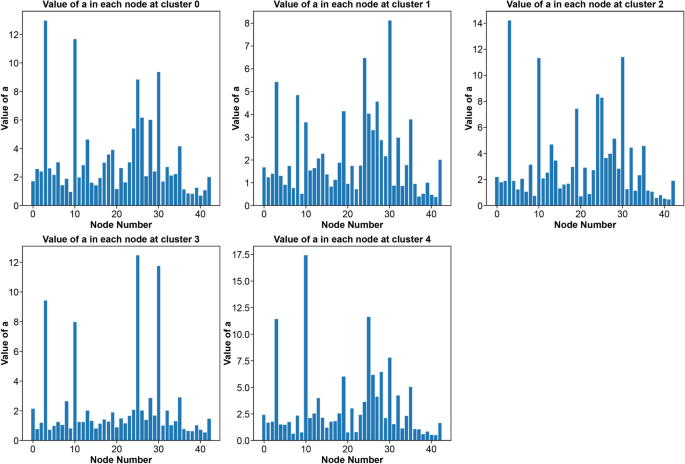
Stay rate for each class
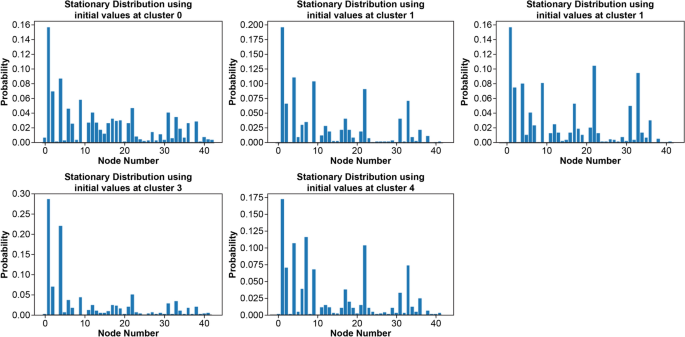
Stationary distribution for each class
Implementation of intra-facility crowdedness optimization
The pre-optimized intra-facility crowding for all users was 0.00157494. Table 6 presents the information on the optimization computing environment. The number of iterations was 1502, and the computation time was 3196.20 s. The intra-facility crowding after optimization was 0.00109697. The total mean stay time is a non-varying constraint; therefore, we checked the mean and standard deviation of the stay rate and the change in the intra-facility crowdedness in each class, as shown in Table 11. It can be observed that the optimization caused a decrease in the overall intra-facility crowdedness as well as the cluster-specific intra-facility crowdedness.
Figure 5 depicts the change in the stay rate before and after optimization. The negative values indicate buildings where the stay rate increased. The stay rates for Building 1 decreased compared to the values in Figs. 3 and 4, indicating that the stay time is longer and the value of the stationary distribution is greater for all classes. The optimization increases the stay rate and reduces the stay time to standardize the value of the stationary distribution of this building, as shown in Fig. 5. Furthermore, it reduces the stationary distribution, as shown in Fig. 6. In Building 30, the stay rate was high, and the stationary distribution was low. After optimization, the stationary distribution could be increased by decreasing the stay rate in classes 0, 2, and 4 and increasing it in classes 1 and 3. Therefore, the increase or decrease in the stay rate, even for the same building, varies based on the class, demonstrating that this method can provide realistic optimization results.
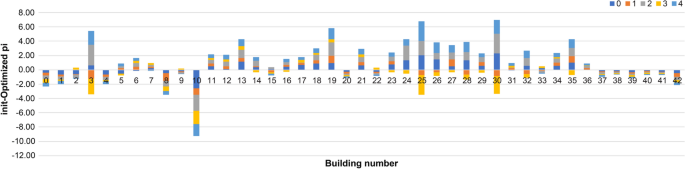
Change in stay rate in each class before and after optimization
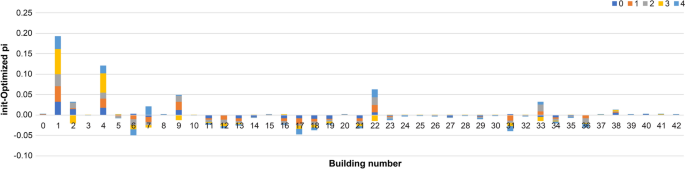
Change in stationary distribution for each class before and after optimization
Conclusion
In this study, we presented a computational algorithm and its environment for effectively using huge Wi-Fi logs and classified the Wi-Fi users based on clustering. We also proposed an optimization model by applying the transition probability matrix and stay rate obtained from Wi-Fi logs to a continuous-time Markov chain. This optimization model can effectively prevent intra-facility crowding, as demonstrated through numerical calculations. The model can reduce the crowding in the facility without changing the transition probability matrix, i.e., without changing the flow line of people and only changing the stay rate. Additionally, the model can be easily adopted for facility management as the optimization can be performed for each user class. The proposed optimization model utilizes Wi-Fi logs to prevent user crowding and simultaneously increases the effectiveness of the facility operations while preventing the transmission of COVID-19.
The main limitation of this study is that there is no disconnection time available in the Wi-Fi logs. Therefore, we have set 3 h as the maximum time spent. If there is no Wi-Fi cut-off time, the accuracy can be improved by performing survival time analysis [47] on the time spent. The objective function of the optimization model is the variance of the stationary distribution. Ohsaki [46] uses an objective function that considers the facility area and the number of people the facility can accommodate. It is essential to compare this with an objective function that includes the structure of the facility.
References
-
Hatabu A, Mao X, Zhou Y, Kawashita N, Wen Z, Ueda M, et al. Knowledge, attitudes, and practices toward COVID-19 among university students in Japan and associated factors: an online cross-sectional survey. PLoS ONE. 2020;15: e0244350. https://doi.org/10.1371/journal.pone.0244350.
-
Stopher PR. Reducing road congestion: a reality check. Transp Policy. 2004;11:117–31. https://doi.org/10.1016/j.tranpol.2003.09.002.
-
Yahiaoui T, Meurie C, Khoudour L, Cabestaing F. A people counting system based on dense and close stereovision. In: Elmoataz A, Lezoray O, Nouboud F, Mammass D, editors. Image and signal processing. Berlin: Springer; 2008. p. 59–66.
-
Eshel R, Moses Y. Tracking in a dense crowd using multiple cameras. Int J Comput Vis. 2010;88:129–43. https://doi.org/10.1007/s11263-009-0307-0.
-
Glueck DH, Karimpour-Fard A, Mandel J, Muller KE. Probabilities for separating sets of order statistics. Statistics. 2010;44:145–53. https://doi.org/10.1080/02331880902986984.
-
Information and communications in Japan 2018. https://www.soumu.go.jp/johotsusintokei/whitepaper/eng/WP2019/2019-index.html. Accessed 29 Dec 2021.
-
Abdul Kader M, Nayim Uddin M, Mohammad Arfi A, Islam N. Anisuzzaman Md. Design amp; Implementation of an automated reminder medicine box for old people and hospital. Eng Technol (ICISET). 2018 International Conference on Innovations in Science; 2018. p. 390–4.
-
Li B, Yu J. Research and application on the smart home based on component technologies and Internet of things. Procedia Eng. 2011;15:2087–92. https://doi.org/10.1016/j.proeng.2011.08.390.
-
Yang M, Huang H, Yuan H, Sun Q. Interaction design of products for the elderly in smart home under the mode of medical care and pension. In: Zhou J, Salvendy G, editors. Human aspects of IT for the aged population healthy and active aging. Cham: Springer International Publishing; 2016. p. 145–56.
-
Hwang I, Jang YJ. Process mining to discover shoppers' pathways at a fashion retail store using a WiFi-base indoor positioning system. IEEE Trans Autom Sci Eng. 2017;14:1786–92. https://doi.org/10.1109/TASE.2017.2692961.
-
Kianoush S, Savazzi S, Rampa V, Nicoli M. People counting by dense WiFi MIMO networks: channel features and machine learning algorithms. Sensors. 2019;19:3450. https://doi.org/10.3390/s19163450.
-
Trivedi A, Zakaria C, Balan R, Becker A, Corey G, Shenoy P. WiFiTrace: network-based contact tracing for infectious diseases using passive WiFi sensing. Proc ACM Interact Mob Wearable Ubiquitous Technol. 2021;5:1–26. https://doi.org/10.1145/3448084.
-
Meneses F, Moreira A. Large scale movement analysis from WiFi based location data. In: 2012 international conference on indoor positioning and indoor navigation (IPIN). 2012. p. 1–9.
-
Vu L, Nguyen P, Nahrstedt K, Richerzhagen B. Characterizing and modeling people movement from mobile phone sensing traces. Pervasive Mob Comput. 2015;17:220–35. https://doi.org/10.1016/j.pmcj.2014.12.001.
-
Zola E, Barcelo-Arroyo F. A comparative analysis of the user behavior in academic WiFi networks. In: Proceedings of the 6th ACM workshop on performance monitoring and measurement of heterogeneous wireless and wired networks 2011;Oct 31:(p. 59–66).
-
Redondi AE, Cesana M, Weibel DM, Fitzgerald E. Understanding the WiFi usage of university students; 2016. International wireless communications and mobile computing conference (IWCMC). http://ieeexplore.ieee.org/document/7577031/. Paphos, Cyprus: IEEE Publications. p. 44–9. Accessed 19 Feb 2022.
-
Basalamah A. Crowd mobility analysis using WiFi sniffers. IJACSA. 2016. http://thesai.org/Publications/ViewPaper?Volume=7&Issue=12&Code=ijacsa&SerialNo=49.7. Accessed 19 Feb 2022.
-
Danalet A, Tinguely L, de Lapparent Md, Bierlaire M. Location choice with longitudinal WiFi data. J Choice Modell. 2016;18:1–17. https://doi.org/10.1016/j.jocm.2016.04.003.
-
Malloy ML, Hartung L, Wangen S, Banerjee S. Network-side digital contact tracing on a large university campus. arXiv preprint https://arxiv.org/abs/2201.10641. 2022.
-
Ruiz-Ruiz AJ, Blunck H, Prentow TS, Stisen A, Kjærgaard MB. Analysis methods for extracting knowledge from large-scale WiFi monitoring to inform building facility planning. In: IEEE Int Conf Pervasive Comput Commun (PerCom). 2014. p. 130–8.
-
Nakanishi W, Kobayashi H, Tsuru T, Matsumoto T, Tanaka K, Suga Y, et al. Understanding travel pattern of tourists from Wi-Fi probe requests: a case study in Motobu Peninsula, Okinawa. JSCE Ser. 2018;D3(74):787–97. https://doi.org/10.2208/jscejipm.74.I_787.
-
Ryu S, Park BB, El-Tawab S. WiFi sensing system for monitoring public transportation ridership: a case study. KSCE J Civ Eng. 2020;24:3092–104. https://doi.org/10.1007/s12205-020-0316-7.
-
Nguemdjo U, Meno F, Dongfack A, Ventelou B. Simulating the progression of the COVID-19 disease in Cameroon using SIR models. PLoS ONE. 2020;15: e0237832. https://doi.org/10.1371/journal.pone.0237832.
-
Shlayan N, Kurkcu A, Ozbay K. Exploring pedestrian Bluetooth and WiFi detection at public transportation terminals. In: 2016 19th International Conference on Intelligent Transportation Systems (ITSC). IEEE Publications. 2016. p. 229–34.
-
El-Tawab S, Yorio Z, Salman A, Oram R, Park BB. Origin-destination tracking analysis of an intelligent transit bus system using Internet of things. In: 2019 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops). 2019. p. 139–44.
-
Arreeras T, Arimura M, Asada T, Arreeras S. Association rule mining tourist-attractive destinations for the sustainable development of a large tourism area in Hokkaido using Wi-Fi tracking data. Sustainability. 2019;11:3967.
-
Gavalas D, Kasapakis V, Konstantopoulos C, Mastakas K, Pantziou G. A survey on mobile tourism Recommender Systems. In: 2013 third international conference on communications and information technology (ICCIT). 2013. p. 131–5.
-
Arreeras T, Endo M, Takahashi H, Asada T, Arimura M. An association rule mining-based exploration of travel patterns in wide tourism areas using a Wi-Fi package sensing survey. J East Asia Soc Transp Stud. 2019;13:1099–113.
-
Gabe A, Kamiya D, Yamanaka R, Fukuda D, Suga Y. Trial of Wi-Fi packet sensing for surveying tourists travel behavior remote islands: A Case Study in Yaeyama Islands. In: Proceedings of the fuzzy system symposium. 35. Japan Society for Fuzzy Theory and Intelligent Informatics. 2019. p. 479–81 (in Japanese).
-
Dantsuji T, Sugishita K, Fukuda D, Asano M. Analysis of the properties of tourists' dwell time using Wi-Fi packet data: a case study of the approach to Hase-dera temple. J City Plan Inst Jpn. 2017;52:247–54. https://doi.org/10.11361/journalcpij.52.247.
-
Alessandrini A, Gioia C, Sermi F, Sofos I, Tarchi D, Vespe M. WiFi positioning and Big Data to monitor flows of people on a wide scale. In: 2017 Eur Navig Conference (ENC). 2017. p. 322–8.
-
Pengjia T, Junhuai L, Huaijun W, Kan W, Yuan Y. Epidemic contact tracing with campus WiFi network and smartphone-based pedestrian dead reckoning. IEEE Sens J. 2021;21(17):19255–67.
-
COVID-19 impacts on transport. https://opendata-nzta.opendata.arcgis.com/datasets/covid-19-impacts-on-transport. Accessed 21 Dec 2021.
-
Ainslie KEC, Walters CE, Fu H, Bhatia S, Wang H, Xi X, et al. Evidence of initial success for China exiting COVID-19 social distancing policy after achieving containment. Wellcome Open Res. 2020;5:81. https://doi.org/10.12688/wellcomeopenres.15843.2.
-
Conrow L, Campbell M, Kingham S. Transport changes and COVID-19: from present impacts to future possibilities. N Z Geogr. 2021;77:185–90. https://doi.org/10.1111/nzg.12315.10.1111/nzg.12315.
-
Zhong L, Mu L, Li J, Wang J, Yin Z, Liu D. Early prediction of the 2019 novel coronavirus outbreak in the Mainland China based on simple mathematical model. IEEE Access. 2020;8:51761–9. https://doi.org/10.1109/ACCESS.2020.2979599.
-
Ndiaye BM, Tendeng L, Seck D. Analysis of the COVID-19 pandemic by SIR model and machine learning technics for forecasting. 2020. https://arxiv.org/abs/2004.01574v1. Accessed 25 May 2021.
-
Simha A, Prasad RV, Narayana S. A simple Stochastic SIR model for COVID 19 Infection Dynamics for Karnataka: Learning from Europe. 2020. [math, q-bio]. http://arxiv.org/abs/2003.11920. Accessed 21 Dec 2021.
-
Shroff NB, Lin Z, Xuan D, Liu F, Ren W, Singh R. A blueprint for effective pandemic mitigation. ITU J-FET. 2020;1:89–101. https://doi.org/10.52953/MJUY7335.
-
Shuja J, Alanazi E, Alasmary W, Abdulaziz A. COVID-19 open source data sets: a comprehensive survey. Appl Intell. 2021;51:1296–325. https://doi.org/10.1007/s10489-020-01862-6.
-
Malloy M, Cahn A, Koller J. Digital Contact Tracing Using IP Colocation. In 2021 IEEE international conference on internet of things and intelligence systems (IoTaIS). 2021 November. p. 73–78.
-
Wang H, Ghosh A, Ding J, Sarkar R, Gao J. Heterogeneous interventions reduce the spread of COVID-19. In: Simul Real Mob Data Arxiv. [physics]. http://arxiv.org/abs/2008.06549. Accessed 29 Dec 2021.
-
Pajevic L, Karlsson G, Fodor V. CRAWDAD dataset Kth/campus (v.2019-07-01). CRAWDAD Wirel Network Data Arch. 2019. https://doi.org/10.15783/c7-5r6x-4b46. Accessed 29 Dec 2021.
-
Cybermedia Center, SQUID. http://www.hpc.cmc.osaka-u.ac.jp/squid/. Accessed 21 Dec 2021 (in Japanese).
-
Miyazawa M. Kindai kagaku sha Co., Ltd, probability and probability process (Modern Mathematics Seminar); 1993.
-
Ohsaki M. Facility layout optimization based on markov chain model and genetic algorithms. J Archit Plan (Trans AIJ). 1998;63:251–8. https://doi.org/10.3130/aija.63.251_1.
-
Kleinbaum DG, Klein M. Survival analysis: a self-learning text. 3rd ed. New York: Springer Science+Business Media; 2012. https://doi.org/10.2307/2532873.
Source: https://link.springer.com/article/10.1007/s43926-022-00026-x
0 Response to "Continuous time Markov Chains Cellular Network Design Solution"
Post a Comment